Projective Geometry

Mathematics behind projective geometry.

1. Alternative Interpretations of Lines

$$ax + by + c = 0$$

Represent it in dot product: $$[a \quad b \quad c] \cdot [x \quad y \quad 1] = 0$$ An alternative definition of the dot product: $$\pmb{a} \cdot \pmb{b} = ||\pmb{a}||||\pmb{b}|| \cos \theta$$ This indicates that the vector $[a \quad b \quad c]$ is perpendicular to every point (x,y) in the $z=1$ plane, or the ray passing through the origin and the point $(x, y, 1)$

We can also define the line by its distance from the origin $d$, and normal vector $\pmb{\hat{n}} = [n_x, n_y]$

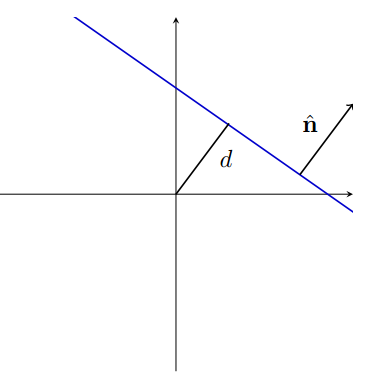
So a line can be represented as $[a \quad b \quad c]$ or $[n_x, n_y, -d]$

2. Point-line Duality

We can represent any line on our image plane by a point in the world using its constants. The point defines a normal vector for a plane passing through the origin that creates the line where it intersects the image plane.

A line is a plane of rays through origin defined by the normal $l = (a, b, c)$. All rays (x,y,z) satisfying: $ax + by + cz = 0$

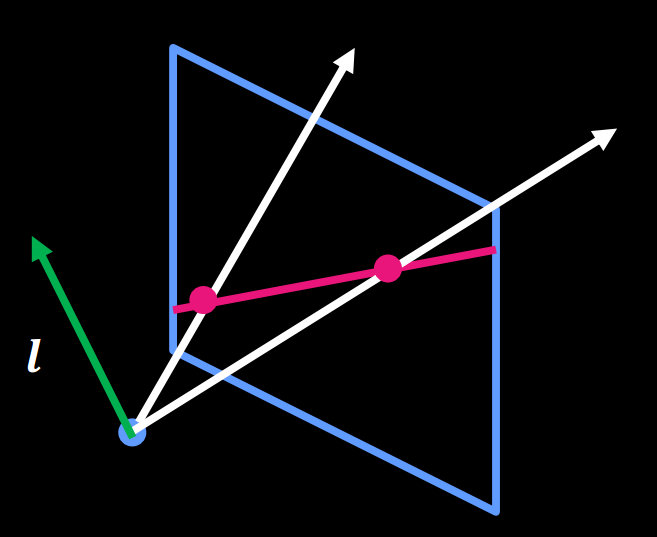
3. Point and line duality

A line $l$ is a homogeneous 3-vector, it is perpendicular to every point (ray) $p$ on the line: $l^T p = 0$

3.1 Points to line

$$l = p_1 \times p_2$$

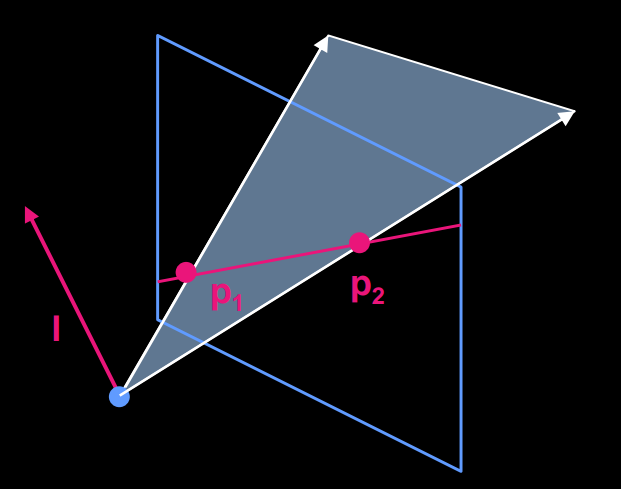
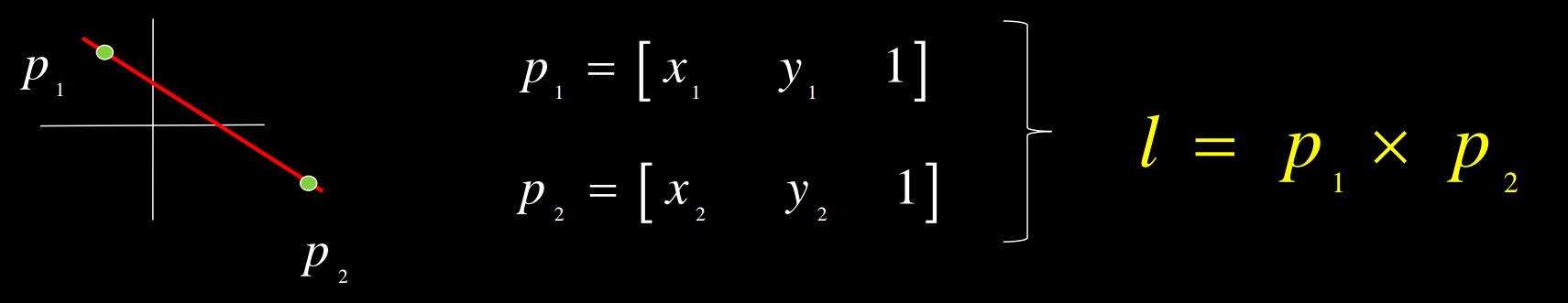
3.2 Lines to Point

$$p = l_1 \times l_2$$

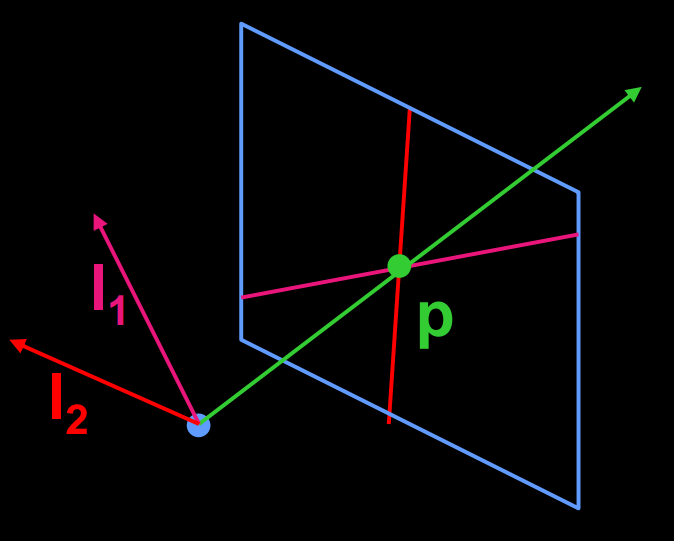
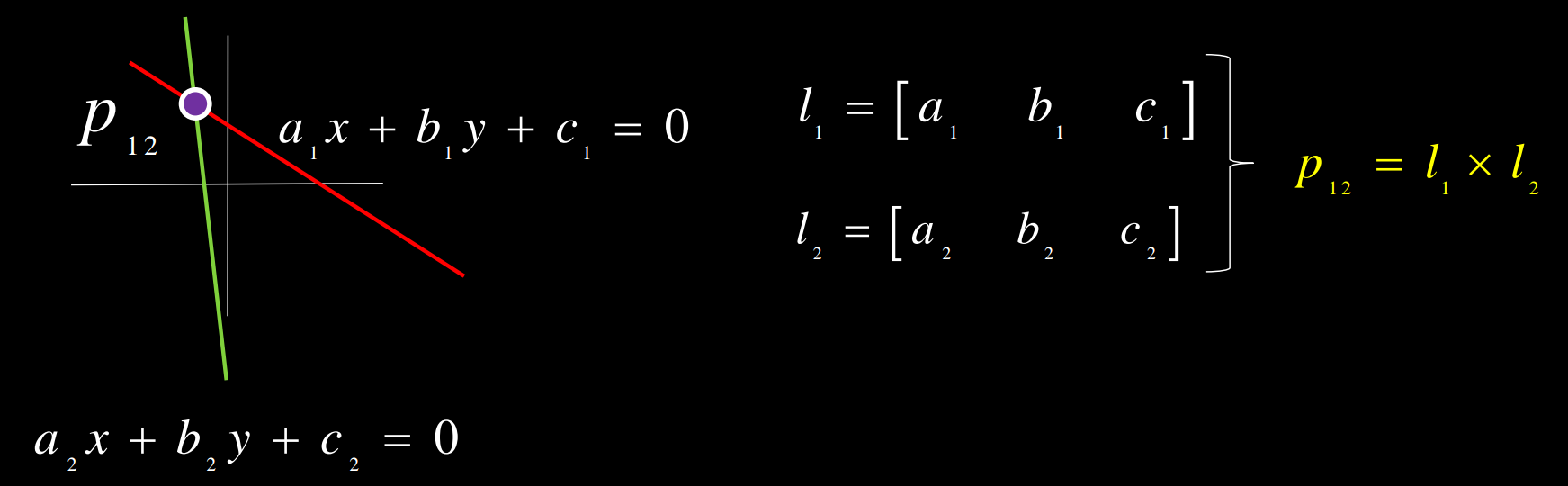
Points and lines are dual in projective space

• Given any formula, can switch the meanings of points and lines to get another formula

3. Ideal Points and Lines

3.1 Ideal Points

Point at infinity

$p = (x, y, 0)$ - parallel to image plane. It has infinite image coordinates

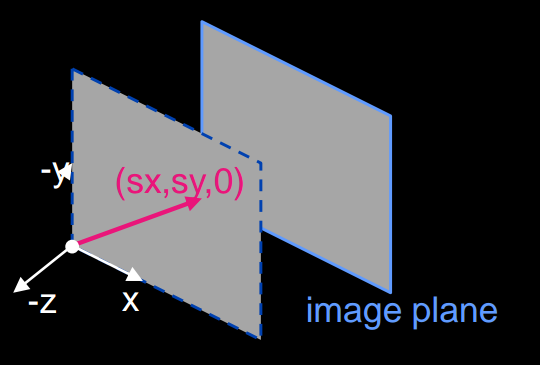
3.2 Ideal Line

$I = (a, b, 0)$ - normal is parallel to image plane. Corresponds to a line in the image (finite coordinates)

• Goes through image origin (principle point)

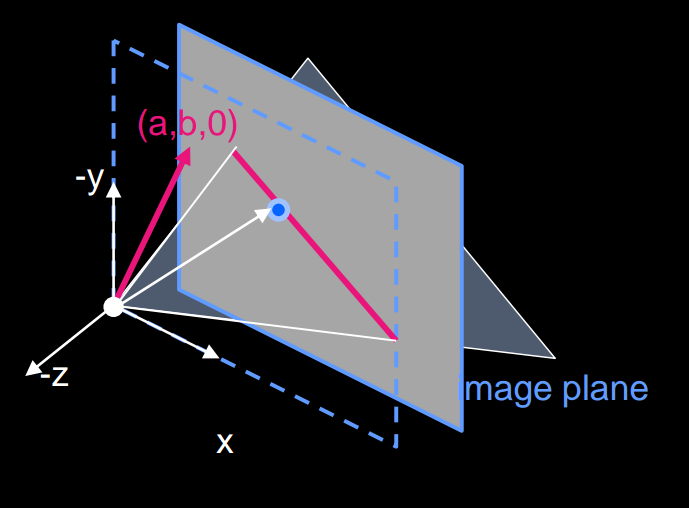
4. Duality in 3D

We can extend this notion of point-line duality int 3D

Recall the equation of a plane: $$ax + by + cz + d = 0$$

where $(a, b, c)$ is the normal of the plane, and $d = ax_0 + by_0 + cz_0$ for some point on the plane $(x_0, y_0, z_0)$.

A plane $N$ is defined by a 4-vector $[a, b, c, d]$, and so $\pmb{N} \cdot \pmb{p} = 0$